Класически метод

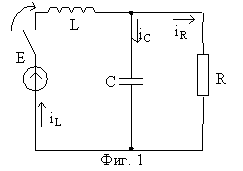
Решаването на задачи от преходни процеси в електрическите вериги се характеризира с някои особености, което налага добро познаване на методите за решаване на задачите от установени режими и използването на сложния математичния апарат за решаване на диференциални уравнения. Многообразието на задачите, зависи от това дали източниците на електродвижещи сигнали са постоянни или променливи, топологията на електрическата верига, броя и вида на реактивните елементи. Всичко това се отразява на конкретния вид и реда на системата от диференциални уравнения, удовлетворяваща преходния процес в електрическата верига. Независимо от това решението се подчинява на определени правила и последователност, които са приложени към примерна електрическа верига, чиято схема е показана на фиг.1.

За веригата показана на схемата e дадено:

E = 100,V ; L = 40/3,mH ; C = 25,; R = 10, .

Търси се: Изменението на напрежението върху изводите на кондезатора и токът през резистора след затваряне на ключа.

1. ОПРЕДЕЛЯНЕ НА НЕЗАВИСИМИТЕ НАЧАЛНИ УСЛОВИЯ

В разглежданата верига те са нулеви т.е. :

и , ( 1 )

защото преди комутацията ( отворен ключ ), токът през бобината и напрежението на изводите на кондензатора са равни на нула.

Забележка: За електрически вериги в които и / или са различни от нула, началните условия се определят от установения режим във веригата преди комутацията.

2. СЪСТАВЯНЕ НА СИСТЕМАТА ОТ ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ ОПИСВАЩИ ПРЕХОДНИЯ ПРОЦЕС В ЕЛЕКТРИЧЕСКАТА ВЕРИГА

По законите на Кирхоф се записва:

( 2 )

от където системата от диференциални уравнения придобива вида:

( 3 )

3. НАМИРАНЕ НА ХАРАКТЕРИСТИЧНОТО УРАВНЕНИЕ

Комутацията в даден клон от електрическата верига предизвиква преходен процес в цялата верига. За да определим интересуващата ни преходна функция в съответния клон, трябва използвайки ( 3 ) да получим диференциалното уравнение, което я описва. На базата на полученото диференциалното уравнение се записва неговото характеристично уравнение, което е необходимо за решаване на първото.

Забележка: Преходните процеси в линейни електрически вериги се описват с линейни диференциални уравнения с постоянни коефициенти [1].

Диференциалното уравнение описващо изменението на напрежението през кондензатора по време на преходния процес е от втори ред и се получава по следния начин:

• диференцира се първото уравнение на ( 3 ) :

. ( 4 )

• замества се

, ( 5 )

определено от второто уравнение на ( 3 ) в ( 4 ) и се получава търсеното нехомогенно диференциално уравнение:

( 6 )

Характеристичното уравнение на хомогенното диференциално уравнение

( уравнение ( 6 ) приравнено на нула ) e от втора степен и има вида:

( 7 )

Известни са и други начини за определяне на характеристичното уравнение[2]:

- посредством алгебраизация на системата ( 3 ).

Състои се в заместване на операцията диференциране с к ( ):

( 8 )

След приравняване на нула на детерминантата ( 9 ) , образувана от

( 9 )

коефициентите пред символичните неизвестни и се стига до същото характеристично уравнение ( 7 ).

След намирането му ( 10 ), комплексния импеданс - се приравнява на нула и

се замества . Полученото уравнение е характеристичното уравнение на ( 6 ) и има същия вид като ( 7 ).

Последните два начина, макар и косвени , позволяват по- лесно определяне на характеристичното уравнение.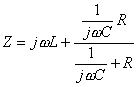

( 10 )

4. РЕШАВАНЕ НА ХАРАКТЕРИСТИЧНОТО УРАВНЕНИЕ

След заместване на L , C и R в ( 7 ) се решава уравнението и се получават два

реални корена ( к₁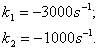к₂ ; дискриминантата D>0 ), което съответствува на апериодичен режим.

( 11 )

Забележка: Съотношението на параметрите – R , L и С на електрическата верига оказва влияние на скоростта на преходния процес. Коефициентите пред променливата к в ( 7 ) са функция на тези параметри и в този смисъл стойностите им са показател за времетраенето на преходния процес - .

1. РЕШАВАНЕ НА ДИФЕРЕНЦИАЛНОТО УРАВНЕНИЕ

Диференциалното уравнение ( 6 ) е нехомогенно ( дясна част 0 ). Общия вид

на решението му ( общия интеграл ) е от вида [1]:

, ( 12 )

където:

решение на нехомогенното диференциално уравнение ( 7 ) или неговия общ интеграл;

установена (стационарна ) съставка или частен интеграл на нехомогенното диференциално уравнение ;

преходна съставка или общ интеграл на хомогенното диференциално уравнение ;

интеграционни константи.

Забележка: Когато характеристичното уравнение ( 7 ) има кратни корени - критично апериодичен режим ( к₁=к₂ ;D=0 ) или комплексни корени – псевдопериодичен режим ( D<0 ), общия вид на решението е различен от ( 12 )[3].

2. НАМИРАНЕ НА ИНТЕГРАЦИОННИТЕ КОНСТАНТИ

- полага се в ( 12 ) t = 0 и като се вземат в предвид независимите начални

условия ( 1 ) се получава:

( 13 )

- диференцира се ( 12 ), полага се t = 0 и се стига до израза:

. ( 14 )

Ако се определи производната 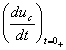, която се явява зависиво начално условие, може да се състави система от алгебричните уравнения ( 13 ) и ( 14 ) и да се пресметне А₁ и А₂ .

Забележка: Зависимите начални условия се намират , като се реши системата уравнения, съставена за момента и се използват независимите начални условия , началните стойности на електродвижещите източници и параметрите на веригата.

- пресмята се производната , като в първото уравнение на ( 3 ) се

полага t = 0₊ и използвайки независимите начални условия ( 1 ) се получава:

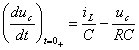( 15 )

• решава се системата ( 16 ) и се получава А₁ = 50,V и А₂ = - 150,V.

( 16 )

1. НАМИРАНЕ НА ОКОНЧАТЕЛНОТО РЕШЕНИЕ НА ЗАДАЧАТА

След заместване на E, A₁, A₂, k₁, и k₂ в ( 12 ), за преходната функция на

напрежението през кондензатора - u_c (t) се получава:

. ( 17 )

Преходната функция на тока – i_R (t) през клона с резистора R e:

. ( 18 )

Също така може да се намерят , като се диференцира ( 17 ) и и C се заместят в първото уравнение на ( 3 ) и като умножим по капацитета на кондезатора С. Полагането на t = 0 в ( 18 ), дава установената съставка на тока - I през резистора R след затихване на преходния процес.

Забележка: Преходният процес теоритично затихва за безкрайно дълго време.В действителност това става за крайно време от порядъка на 5. За конкретната задача след затихване на реходния процес, кондензаторът се е заредил до напрежението на източника , , а токът I се ограничава единствено от съпротивлението на резистора R . На практика веригата се се редуцира до едноконтурна.

2. ИЗОБРАЗЯВАНЕ НА РЕШЕНИЕТО В ГРАФИЧНА ФОРМА

На фиг.2 е изобразено изменението на , и , а на фиг. 3 -

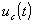
                                     фиг. 2

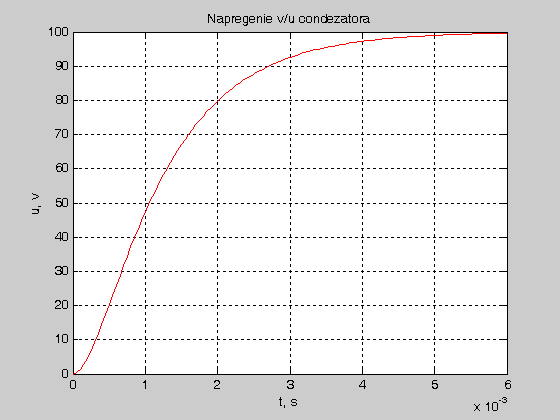
                                         фиг. 3

1. Димова В. и др. Методическо ръководство за решаване на задачи по висша математика – IV част, “ Техника “, София, 1975г.;

2. Бессонов Л. А. Теоритические основы Электротехнники, “Высшая школа”, Москва,1984;

3. Фархи С., Папазов С. Теоритична електротехника – I част, “ Техника “, София, 1987г.;

2006г. Съставил: / гл. ас. инж. Д. Данаилов /

Публикации в периода 2001 – 2009 г.

гл.ас. инж. Данаил Йовчев Данаилов

 1. D. Y. Danailov Three – phase transformer transients . “ MEET ‘ 2002 ” , Varna , 7 – 11.10. 02 y.

2. Д. Данаилов , Ч. Джамбазки Преходен процес при включване на силов трансформатор на празен ход ,

сп. “ Железопътен транспорт “, бр. 1 , 2003 г.

3. Д. Данаилов , Ч. Джамбазки Модернизация на електрическите локомотиви “ Шкода “ с внедряване на Рекуперативно спиране. , сп. “ Железопътен транспорт “, 2003 г.( към 1.11. 2003 г. още не публикувана )

4. Danailov D. Y.Mathematical modelling of transient processes in electric drive circuit : drive substation , contact network , electric locomotive . “ 11 International Scientific Conference, Zilina, 17 – 19 September 2003, Slovak Republic

5. Георги Димитров, Данаил Данаилов, Чавдар Джамбазки Изследване изменението на електрическите загуби в трансформаторните постове във ВТУ “ Тодор Каблешков “ при различни схеми за захранване на главните консуматори. Тринадесета научна конференция –“Транспорт 2003 “,13 – 14 ноември 2003 г. , София.

6. D. Danailov Mathematical model of transient process in three – phase transformer.Forms/Format ‘2004, 2 - 3.12.04, Braunschweig, Germany

7. Danailov D.Y., Danailova R.D., Dimitrov G. I. Simulation Of Transient Process In Three - Phase Transformer.

14^th International Symposium, Eurnex - Zel 2006 “Towards the competitive rail systems in Europe” 30^th - 31^st May 2006 Zilina, Slovak Republic, EU

8. Danailov D. Y. Mathematical Modelling Of Transient Processes In Electric Drive Circuit On Electric Locomotive Mould “ ЉKODA 43 “ . 14^th International Symposium, Eurnex – Zel 2006 “Towards the competitive rail systems in Europe” 30^th - 31^st May 2006 Zilina, Slovak Republic, EU 

НИП на тема:  Математическо   моделиране  на  електромагнитните  преходни процеси  в  нелинейни многоконтурни  тягови електрически вериги  посредством   “ Matlab “

консултации- четвъртък 13.30-15.30